格入门

(Updated: )

格密码

了解和学习中

参考

2012年BIU密码学冬令营-04-Basic Cryptanalysis（中文字幕）_哔哩哔哩_bilibili

DexterJie’Blog

维基百科，自由的百科全书

定义

格(lattice)是一种数学结构，给定一组线性无关的非零基向量 (basis)（称作格基）的整系数线性组合，格就是这些基向量的线性组合

简单来说给定一组格基(向量) a1, a2, …, an，对任意的整数 c1, c2, …, cn，并将其作为格基的系数，则 c1a1, c2a2, …, cnan都是属于这个格的向量，而n为该格的维数。

img

这里的(2,2)就是由向量i(1,0)和向量j(0,1)组成的（2,2)=2i+2j，这就是一个基础的二维格。

再这个二维格上的任意一点都可以由这对基向量组成，所以我们通常用格基代表格，所以就可以写成 而此时我们就可以将（2,2）=2i+2j写成

一些补充定义

基

在向量空间中的每个点，都可以由基的线性变化得到，被称为基向量。 一个格可能会有很多的基并不唯一构成，例子如上。

正交基

两个基直接是相互垂直的

格基规约

找到最接近正交基的基向量

格运算（行列式运算）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
#sage
v1 = [2, 1, 3]
v2 = [1, 2, 0]
v3 = [2, -3, -5]
A = matrix([v1, v2, v3])
print(A)
# [ 2  1  3]
# [ 1  2  0]
# [ 2 -3 -5]
U = matrix([[1, 0, 1], [1, -1, 2], [1, 2, 0]])
print(U)
# [ 1  0  1]
# [ 1 -1  2]
# [ 1  2  0]
print(U.det())#行列式的值
# -1
B = U*A
print(B)
# [ 4 -2 -2]
# [ 5 -7 -7]
# [ 4  5  3]
inv_U = U.inverse() #求矩阵的逆
print(inv_U)
# [ 4 -2 -1]
# [-2  1  1]
# [-3  2  1]
assert inv_U * B == A

所以我们就可以将各种这种向量问题转化为矩阵计算的方式，同样我们可以反过来将计算矩阵转化为空间中的图示。

格密码的难题

而在格学说里，有两个知名难题：

  • SVP (最短向量问题, Shortest Vector Problem): 最短向量问题(The Shortest Vector Problem,SVP)是指在格L中找到一个最短的非零向量，即寻找一个v满足欧几里得范数最小（指该集合的每一个元素的平方和再开方）范数就是指长度

  • CVP (最近向量问题, Closest Vector Problem): 是指一个向量w不在格L中，然后在格L上找到一个向量v与w最接近。

    上面的两个问题都在广义上被证明是 NP-hard 问题，求解起来十分困难，而且会随维数的增加而变得越来越困难。有些问题可以通过对CVP加上一维之后转变为SVP问题，因为SVP相比CVP稍微简单一些

LLL算法

LLL算法（Lenstra-Lenstra-Lovász算法）是一种求解最短向量问题的近似算法。其基本思路是将给定的格分解为一个格基，然后找到一个新的格基，其基向量更短，并且更接近于原格。这个过程可以通过不断地将格分解为更小的子格并找到更短的基向量来实现。

具体的来说就是根据给定的格基通过规约的方式在当前的格的空间中得到一组更简单的格（类似辗转相除的方式），然后优化得到的最优格基便是我们所需要的最短非零向量。

但是LL算法的使用前提要满足Hermite定理

Hermite定理

这个定理给出了最短向量的上界

对于n维的格ℒ, 都包含一个非零向量v⃗ ∈ ℒ, 满足

其中n表示维度，也就是基向量的个数

det(L) = 行列式的值

施密特正交化

这个定理给出了最短向量的下界

其作用是把一组基转换成一组正交基。

img

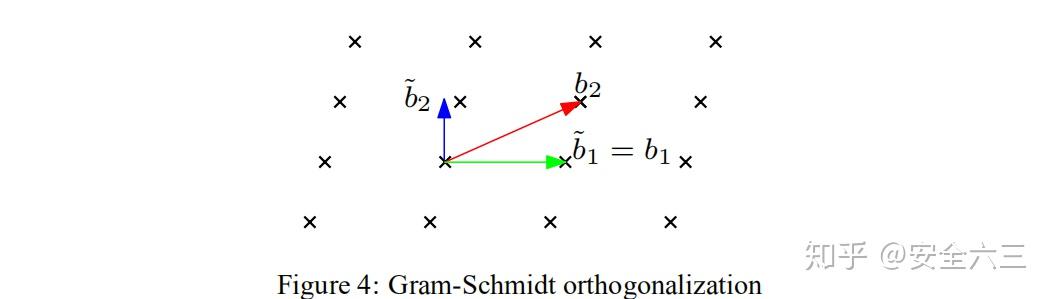
如图所示

将基b1, b2转变为了这组基

过程如下 首先, 给定一组线性无关的向量 然后通过计算得到一组正交基 表示与的内积 我们令 则正交化向量可表示为 但是需要注意的是，施密特正交化得到的结果并不一定在格基上(因为没有限制系数为整数)

施密特正交化应用(QR分解)

对于一组格基先进行施密特正交化，之后我们就能得到一组近似正交基 写成矩阵的形式即是 这是一个主对角线都为正数的上三角行列式，所以行列式的值为

  1. 该矩阵是上三角行列式所以行列式
  2. 我们能得到λ1的下界，即λ1 ≥ min (||b̃i||)

严谨的证明

证明: 设x ∈ ℤn是任意的非零整数向量，让我们证明 . 设 j ∈ 1, 2, …, n是最大值，其中xj ≠ 0。可得 其中，∀i < j, , . 另一方面， , 因此我们得出结论 （不是很理解这个证明的过程，但是至少知道了结论，所以暂时就先用这个结论来理解λ1的下界

LLL算法的应用

在n维空间中，LLL算法实际上即使要让施密特正交化的程度达到最大化

官方解答是，LLL算法要找一个基，使得Gram-Schmidt向量的正交程度不会下降太快

LLL算法的实际运用是这样的 这其实就是施密特正交化的过程如同 B这个基可以写成一个正交向量构成的矩阵，乘上一个幺模矩阵（一个方阵的行列式绝对值为1）

LLL的性质

  • 所有的 |μi, j| ≤ 0.5

  • (这个性质的大致意思是得到的向量不能太短)

由上述两个性质我们可以得到一个结论

LLL的目标就是要得到满足这个要去的基

LLL算法的实施过程

我们有一个基用b表示，写成列向量的形式

中间是施密特正交基

然后在正交基上乘以右边的矩阵才能得到b

如何使|μi, j| ≤ 0.5

减去足够多次的第一列即可满足

如何确保向量下降的不够快

如果下降的过快就与前一列的向量交换位置，然后就会得到一个更好的基（类似于辗转相除的思想）