LFSR

John Doe

2025-07-14 (Updated: 2025-07-15)

建立在他人博客的推文上对于LFSR的初步了解与尝试

定义（流密码 | Lazzaro）

LFSR指给定前一状态的输出，将该输出的线性函数再用作输入的移位寄存器。线性反馈移位寄存器(LFSR)归属于移位寄存器(FSR)。

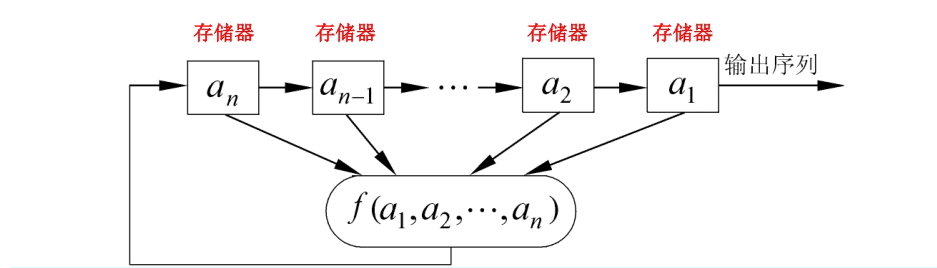
GF(2) 上一个 n 级反馈移位寄存器由 n 个二元存储器与一个反馈函数 f(a1,a2,⋯,an) 组成：

移位寄存器三要素：

初始状态：由用户确定
反馈函数：f(a1,a2,⋯,an) 是 n 元布尔函数，即函数的自变量和因变量只取0和1这两个可能值
输出序列

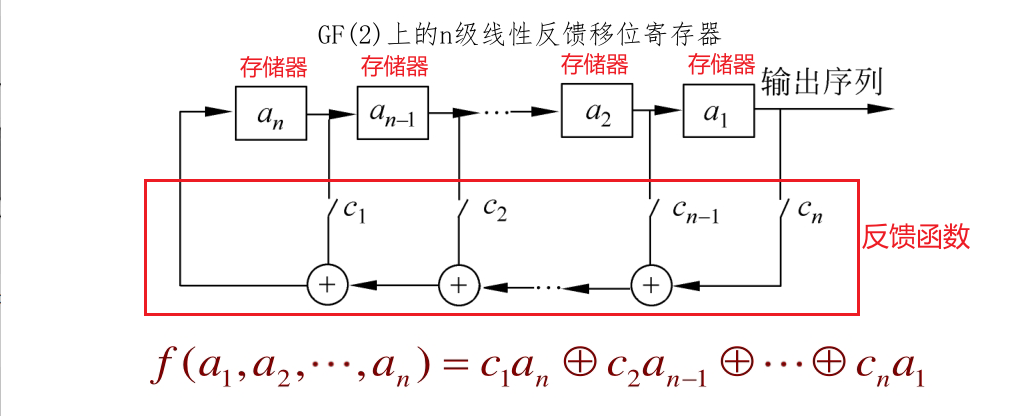
如果反馈函数是线性的，那么我们称其为线性反馈移位寄存器(LFSR)：

LFSR的输出序列 {an} 满足：对于 n 级线性反馈移位寄存器，最长周期为2ⁿ − 1（排除全0），达到最长周期的序列一般称为 m 序列。

实例

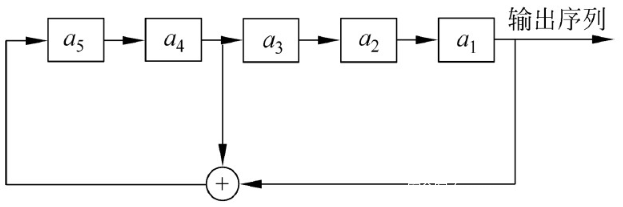
假设给定了一个5级的LFSR，其初始状态（a1到a5这五个二元存储器的值）为

(a₁, a₂, a₃, a₄, a₅) = (1, 0, 0, 1, 1)

它的反馈函数为

f(a₁, a₂, a₃, a₄, a₅) = a₄ ⊕ a₁

它的输出过程如下

然后 a₆ = a₄ ⊕ a₁ = 1 ⊕ 1 = 0

a₇ = a₅ ⊕ a₂ = 1 ⊕ 0 = 1

所以我们可以由此推出反馈函数 a_n = a_n − 2 ⊕ a_n − 5 对于一个n级的LFSR来讲，其最大周期为2ⁿ − 1 ，因此对于我们上面的5级LFSR来讲，其最大周期为 2⁵ − 1 = 31.

2018 CISCN 线上赛 oldstreamgame


flag = "flag{xxxxxxxxxxxxxxxx}"
assert flag.startswith("flag{")
assert flag.endswith("}")
assert len(flag)==14

def lfsr(R,mask):
    output = (R << 1) & 0xffffffff
    i=(R&mask)&0xffffffff
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1
    output^=lastbit 
    return (output,lastbit)

R=int(flag[5:-1],16)
mask = 0b10100100000010000000100010010100

f=open("key","w")
for i in range(100):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

已知条件：

flag包裹内容为8位十六进制数字也就是32位二进制数也就是我们需要的求的初态
反馈函数已知要转化成数学表达式
已知输出和mask掩码

def lfsr(R,mask):
    output = (R << 1) & 0xffffffff#先把R左移，然后和0xffffffff进行与操作，其作用是把R的最高位抹去并在最低位补0，并保留低32位，再把该值赋值给output
    i=(R&mask)&0xffffffff#将R和mask进行与操作，并保留低32位，再把该值赋值给i，这一步与output相对独立
    lastbit=0
    while i!=0:
        lastbit^=(i&1)
        i=i>>1#这里是将i的最低位向i的最高位依次做异或运算，这里与1进行的与运算没有影响
    output^=lastbit #将output变量的值和lastbit的值异或，再赋值给output
    return (output,lastbit)

f=open("key","w")
for i in range(100):
    tmp=0
    for j in range(8):
        (R,out)=lfsr(R,mask)
        tmp=(tmp << 1)^out
    f.write(chr(tmp))
f.close()

1
2

key=20FDEEF8A4C9F4083F331DA8238AE5ED083DF0CB0E7A83355696345DF44D7C186C1F459BCE135F1DB6C76775D5DCBAB7A783E48A203C19CA25C22F60AE62B37DE8E40578E3A7787EB429730D95C9E1944288EB3E2E747D8216A4785507A137B413CD690C

对flag做了100次循环得到了100个16进制数

判断

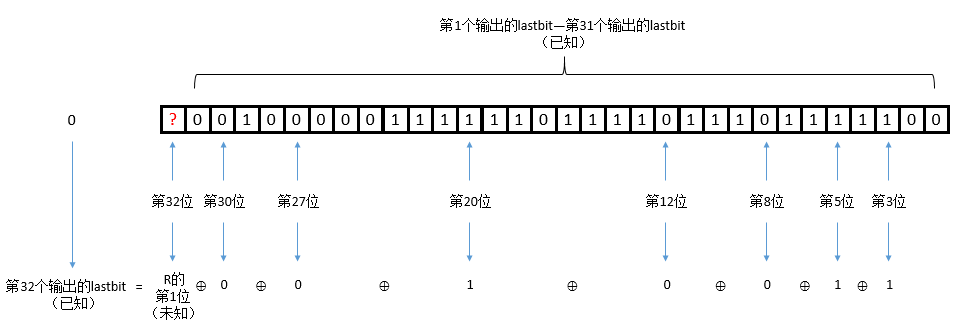
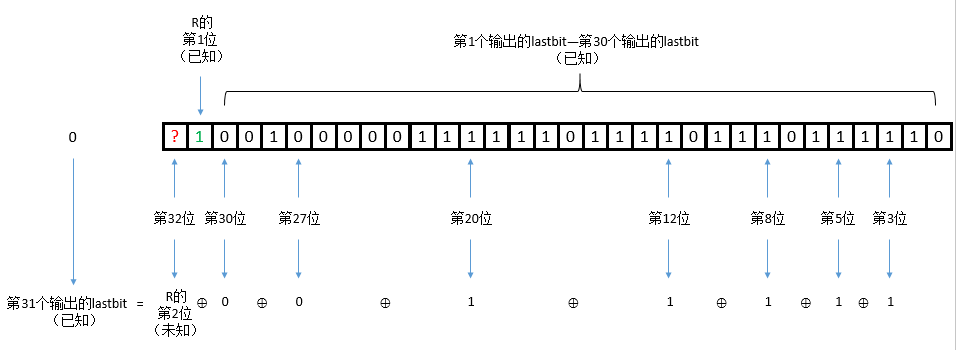
mask只有第3、5、8、12、20、27、30、32这几位为1，其余位均为0。 mask与R做按位与运算得到i，当且仅当R的第3、5、8、12、20、27、30、32这几位中也出现1时，i中才可能出现1，否则i中将全为0。 lastbit是由i的最低位向i的最高位依次做异或运算得到的，在这个过程中，所有为0的位我们可以忽略不计（因为0异或任何数等于任何数本身，不影响最后运算结果），因此lastbit的值仅取决于i中有多少个1：当i中有奇数个1时，lastbit等于1；当i中有偶数个1时，lastbit等于0。当R的第3、5、8、12、20、27、30、32这几位依次异或结果为1时，即R中有奇数个1，因此将导致i中有奇数个1；当R的第3、5、8、12、20、27、30、32这几位依次异或结果为0时，即R中有偶数个1，因此将导致i中有偶数个1。因此我们可以建立出联系：lastbit等于R的第3、5、8、12、20、27、30、32这几位依次异或的结果。写成反馈函数，也就是 lastbit = R₃ ⊕ R₅ ⊕ R₆ ⊕ R₁₂ ⊕ R₂₀ ⊕ R₂₇ ⊕ R₃₀ ⊕ R₃₂ 我们将key全部转成二进制

x='20FDEEF8A4C9F4083F331DA8238AE5ED083DF0CB0E7A83355696345DF44D7C186C1F459BCE135F1DB6C76775D5DCBAB7A783E48A203C19CA25C22F60AE62B37DE8E40578E3A7787EB429730D95C9E1944288EB3E2E747D8216A4785507A137B413CD690C'
b=bin(int(x,16))[2:]
print(b)
print(len(b))
#100000111111011110111011111000101001001100100111110100000010000011111100110011000111011010100000100011100010101110010111101101000010000011110111110000110010110000111001111010100000110011010101010110100101100011010001011101111101000100110101111100000110000110110000011111010001011001101111001110000100110101111100011101101101101100011101100111011101011101010111011100101110101011011110100111100000111110010010001010001000000011110000011001110010100010010111000010001011110110000010101110011000101011001101111101111010001110010000000101011110001110001110100111011110000111111010110100001010010111001100001101100101011100100111100001100101000100001010001000111010110011111000101110011101000111110110000010000101101010010001111000010101010000011110100001001101111011010000010011110011010110100100001100
#798

手动再补充2位0 因为是需要反推32位，所以我们只需要取最高位的前32位数据即可

1	32位Key值：00100000111111011110111011111000

$第个输出的的第位未知$

$第个输出的的第位未知$ 以此类推，R的全部32位我们都可以依次求出了

key = "00100000111111011110111011111000"
mask = "10100100000010000000100010010100"

R = ""
tmp = key

for i in range(32):
    n = '?'+key[:31]
    m = int(n[-3])^int(n[-5])^int(n[-8])^int(n[-12])^int(n[-20])^int(n[-27])^int(n[-30])^int(tmp[-1-i]) 
    R += str(m)
    key = str(m) + key[:31] 

print("flag{"+ hex(int(R[::-1],2)) + "}")
#flag{0x926201d7}

不是很懂，目前先进行一个大概看看，后续有关lfsr的题目再进行补充

2025NPC CTF river

class LFSRStreamCipher:
    def __init__(self, key: int):
        if not (0 <= key < 2**16):
            raise ValueError("Key must be a 16-bit integer")
        self.state = key
        self.poly = 0b1010000000000101  # 反馈多项式: x^16 + x^14 + x^13 + x^11 + 1

    def lfsr_step(self) -> int:
        feedback = self.state & 1
        self.state >>= 1
        if feedback:
            self.state ^= self.poly
        return feedback

    def generate_keystream(self, length: int) -> bytes:
        keystream = bytearray()
        for _ in range(length):
            byte = 0
            for i in range(8):
                byte |= self.lfsr_step() << i
            keystream.append(byte)
        return bytes(keystream)

    def encrypt(self, plaintext: bytes) -> bytes:
        """使用密钥流加密"""
        keystream = self.generate_keystream(len(plaintext))
        return bytes(p ^ k for p, k in zip(plaintext, keystream))

    def decrypt(self, ciphertext: bytes) -> bytes:
        """使用密钥流解密（加密与解密是相同的）"""
        return self.encrypt(ciphertext)


key = 0b1101011010110101
cipher = LFSRStreamCipher(key)


ciphertext = cipher.encrypt(flag)



print("Ciphertext:", ciphertext.hex())



#bd8b802f4a05ed77abace36b6cf9adbe627d3632edff818c556120ad131b50dbedd0f4af4483

常规的LFSR题目，加密方式和反馈多项式都给了，并且因为异或具有可逆性，所以只需要再将密文按照这个逻辑即可解密。需要注意的是要在初始化的时候将LFSR内部重置一下。

from Crypto.Util.number import*


class LFSRStreamCipher:
    def __init__(self, key: int):
        if not (0 <= key < 2**16):
            raise ValueError("Key must be a 16-bit integer")
        self.initial_key = key  
        self.poly = 0b1010000000000101
        self.reset()  

    def reset(self):#重置，确保密钥和解密开始时状态相同
        self.state = self.initial_key

    def lfsr_step(self) -> int:
        feedback = self.state & 1
        self.state >>= 1
        if feedback:
            self.state ^= self.poly
        return feedback

    def generate_keystream(self, length: int) -> bytes:
        keystream = bytearray()
        for _ in range(length):
            byte = 0
            for i in range(8):
                byte |= self.lfsr_step() << i
            keystream.append(byte)
        return bytes(keystream)

    def decrypt(self, ciphertext: bytes) -> bytes:
        self.reset()  
        keystream = self.generate_keystream(len(ciphertext))
        return bytes(p ^ k for p, k in zip(ciphertext,
        keystream)) 

key = 0b1101011010110101
cipher = LFSRStreamCipher(key)

ciphertext = 0xbd8b802f4a05ed77abace36b6cf9adbe627d3632edff818c556120ad131b50dbedd0f4af4483


decrypted = cipher.decrypt(long_to_bytes(ciphertext))

print("Decrypted:", decrypted)

#Decrypted: b'flag{two_dift3rs_0ff_t0_s33_th3_w0rld}'

总结

lfsr的基本原理还是不难看懂的，关键在于各个题目中代码转换成数学公式的能力和反推回去。

码力和理解能力还是太差了(悲